Financial Management
Capital Budgeting
Part A
Definition of capital budgeting
Capital budgeting is a process of identifying,
evaluating and selecting the project/s to be taken up for execution, out of
many such projects to choose from, in such a way that the selection of the
project/s satisfies the following requirements:
1. The selected project/s give/s the best possible returns.
In other words, total return from the selected project/s is more than total
return from the projects not selected;
2. Net present value of cash flows from the project/s
selected is greater than that from the projects not selected;
3. The selected project/s return/s back the initial
investments faster than the projects not selected;
4. The rate of return on investment (ROI) is higher in case
of the selected project/s than the projects not selected;
5. The total capital requirement for investing in the
selected project/s is within the available resources (funds) earmarked for
investment in new projects;
6. The project/s so selected for future investment is/are
in line with the overall objectives and goal of the firm in terms of
maximisation of shareholders’ wealth.
Methods of project evaluation or project appraisal
A number of quantitative techniques have been developed
for evaluating or appraising the capital investment proposals in course of and
for the purpose of capital budgeting, the most important of which are:
A. Traditional methods
1.
Average/Accounting Rate of Return (ARR) method, and
2.
Pay Back (PB) period method.
B. Discounted cash flow methods
1.
Net present value (NPV) method,
2.
Internal rate of return (IRR) method,
3.
Modified internal rate of return (MIRR) method,
4.
Profitability index (PI) method,
5.
Discounted pay back (DPB) period method, and
6.
Terminal value (TV) method.
ARR Method
|
ARR = |
[Average PAT ÷ Average investment] x 100 |
|
Where, |
|
|
Av. PAT = |
(Total of expected PATs for each of the years of the
life of the project) ÷ (Number of years of the life of the project) |
|
Av. Investment = |
Additional net working capital + Salvage value +
[(Initial Investment – Salvage value) ÷ 2] |
Decision criteria:
For a single project under consideration, the project
will be accepted if ARR is higher than the required rate of return (i.e. cost
of capital).
If there are more than one projects each one of them
having ARR which is higher than the required rate of return, the project having
the highest ARR will be selected.
Pay Back Period Method
|
Payback period = |
(Initial investment) ÷ (Uniform annual CIAT) |
|
Where,
CIAT = |
Cash inflow after tax |
The above formula can be applied for calculating payback
period only when the cash flow stream is in the nature of annuity for each year
of the life of the project, i.e. CIATs are uniform. But if the CIATs are not
uniform, then pay back period will be simply the minimum period required to
recover the initial investment from the project. In this case, the minimum
period required to recover the initial investment can be arrived at by
calculating the cumulative CIATs against each year of the life of the project.
Decision criteria:
For a single project under consideration, the project
will be accepted if the payback period calculated for the project is less than
the maximum payback period set by the management.
In case of two or more competing projects (each one
having a payback period less than the maximum set by the management), the
project having the shortest payback period would be selected.
NPV Method
|
NPV = |
∑ PV of all CIATs − ∑ PV of all COs |
|
Where, CIAT = |
Cash inflow after tax |
|
And CO = |
Cash outflow |
Decision criteria:
For a single project under consideration, the project
will be accepted if the NPV of the project is positive, i.e. if NPV > 0.
In case of two or more competing projects, the project
having highest positive NPV would be selected.
IRR Method
IRR, with respect to an investment project, is that discount rate which equates the present value of anticipated future cash inflows from the project to the initial cost of the project (i.e. cash outflow). Accordingly, IRR is also defined as the discount rate at which the NPV is zero.
IRR can be calculated using either of the following
two formulas:
|
1. IRR = |
LR + [(NPV at LR) ÷ (NPV at LR − NPV at HR)] × (HR –
LR) |
|
2. IRR = |
HR − [(NPV at HR) ÷ (NPV at HR − NPV at LR)] × (HR –
LR) |
Where,
|
LR = |
Lower discount rate |
|
HR = |
Higher discount rate |
|
NPV at LR = |
Net Present value of CIATs at lower discount rate |
|
NPV at HR = |
Net Present value of CIATs at higher discount rate |
|
CIAT = |
Cash Inflow after Tax |
Steps to find out LR and HR
STEP: 1
Find required PVIFA (k, n) which, if multiplied by
average CIAT, gives the initial investment so that NPV equals to zero. In other
words, PVIFA (k, n) should be such that,
PVIFA (k, n) = Initial Investment ÷ Average CIAT.
STEP: 2
From the “Present value of an annuity of Rs 1” table
find two PVs of an annuity of Rs 1 closest to PVIFA (k, n) for the life of the
project (i.e. for ‘n’ years).
STEP: 3
From the “Present value of an annuity of Rs 1” table again find the interest rates (i.e. ‘k’ %) corresponding to the two PVs as identified in STEP: 2. If the CIATs are uniform, the interest rate against the higher PV is LR and the interest rate against the lower PV is HR; and STEP: 4 is not required.
Alternative to Steps 1, 2 and 3:
Computation of Internal Rate of Return (IRR) –
Shortcut Method – applicable only when there is single cash outflow in the form
of initial investment
Find out initial LR and initial HR by calculating the
value of ‘r’ as follows:
STEP: 1
Compute the value of ‘r’ as follows:
|
r = |
[(A/I) ^ {2/ (N+1)} – 1]
× 100% |
Where,
|
A = |
Sum of the inflows |
|
I = |
Initial investment (i.e. single outflow) |
|
N = |
Number of years of the project life |
STEP: 2
Calculate NPV taking the
rounded off value of ‘r’ as discount rate.
STEP: 3
If the NPV calculated in
STEP: 2 is (+)ve, increase the discount rate by 1 percentage point and
calculate new NPV with this new discount rate. But, if the NPV calculated in
STEP: 2 is (−)ve, decrease the discount rate by 1 percentage point and
calculate new NPV with this new discount rate.
Discount rate as stated in
STEP: 2 and in this STEP: 3 are initial discount rates – one is Initial LR and
the other is Initial HR in accordance with the value of NPV calculated in STEP:
2.
STEP: 4
Find the NPV of the project using both the approximate
interest rates as identified in STEP: 3 above. Now on the basis of the NPVs so
calculated three alternative courses of action
will follow.
First alternative:
If the lower interest rate (Initial LR)
gives positive NPV and the higher interest rate (Initial HR) gives negative
NPV, the Initial LR is the Final LR and the Initial HR is the Final HR.
Second alternative:
If both the NPVs are positive, try a higher interest rate which can be identified
as:
|
New IR = |
Initial HR + [(NPV at Initial HR) ÷ (NPV at Initial
LR – NPV at Initial HR)] |
Find NPV using this new-found interest rate.
(a) If this new NPV is positive, increase the interest
rate by one. This process should be carried on until the NPV becomes negative.
(b) If this new NPV is negative, reduce the interest rate
by one. This process should be carried on until the NPV becomes positive. IRR should lie between two such consecutive interest
rates that one of the rates (the lower one) gives positive NPV and the other
one (the higher one) gives negative NPV.
Third alternative:
If both the NPVs are negative, try a lower interest rate which can be identified as:
|
New IR = |
Initial LR – [(NPV at Initial LR) ÷ (NPV at Initial
HR − NPV at Initial LR)] |
Find NPV using this new-found interest rate.
(a) If this new NPV is negative, reduce the interest rate
by one. This process should be carried on until the NPV becomes positive.
(b) If this new NPV is positive, increase the interest
rate by one. This process should be carried on until the NPV becomes negative. IRR should lie between two such consecutive interest
rates that one of the rates (the lower one) gives positive NPV and the other
one (the higher one) gives negative NPV.
Decision criteria:
IRR is the maximum rate of interest which an
organisation can afford to pay on the capital invested in a project. Therefore,
a project is acceptable, if its IRR is greater than the cost of capital (k). On
the other hand, a project should be rejected, if its IRR is less than the cost
of capital (k). But if the IRR of a project is equal to the cost of capital
(k), the firm may remain indifferent, i.e. the project may be or may not be
accepted.
Symbolically,
1. If IRR > k, the project is acceptable,
2. If IRR < k, the project is not acceptable, and
3. If IRR = k, the project may be or may not be accepted.
In case of two or more competing projects, the project
giving the highest IRR (which should also necessarily be higher than the cost
of capital) would be selected.
MIRR Method
Modified internal rate of return (MIRR) is a method of
evaluating the profitability of capital investment proposals. MIRR can be
calculated using the following two formulas:
|
1. |
MIRR = |
[(∑ PV of all CIATs) ÷ (∑ PV of all Cash
Outflows)]^(1/n) x (1+i) – 1 |
|
|
Where, |
|
|
|
PV = |
Present value, discount rate being the cost of
capital |
|
|
n = |
Number of years of the project |
|
|
i = |
Cost of capital of the company / firm |
|
2. |
MIRR = |
(Terminal Value of the Project / ∑
PV of all Cash Outflows)^(1/n) – 1 |
Decision criteria:
MIRR is the maximum rate of interest which an
organisation can afford to pay on the capital invested in a project. Therefore,
a project must be accepted if its MIRR is higher than the cost of capital (k).
On the other hand, a project shall be rejected if its MIRR is less than the
cost of capital (k). But if the MIRR of a project is equal to the cost of
capital (k), the firm may remain indifferent.
In case of two or more competing projects, the project
giving the highest MIRR (which should also necessarily be higher than the cost
of capital) would be selected.
PI Method
|
PI = |
(∑ PV of all cash inflows after tax) ÷ (∑ PV of all
cash outflows) |
|
= |
(∑ PV of all CIATs) ÷ (∑ PV of all COs) |
Decision criteria:
For a single project under consideration, the project
will be accepted if the PI is more than one. But the project will be rejected
in case the PI is less than one. However, if the PI is equal to one, the firm
may remain indifferent.
In case of two or more competing projects (each one
having its PI > 1), the project having highest PI would be selected.
Discounted Pay Back Period Method
Under this method the present values of all cash
outflows and inflows are computed at an appropriate discount rate (normally,
cost of capital). The present values of all inflows are cumulated in order of
time. The time period at which the cumulated present value of cash inflows
equals to the present value of cash outflows is known as discounted payback
period.
Decision criteria:
For a single project under consideration, the project
will be accepted if the discounted payback period calculated for the project is
less than the maximum discounted payback period set by the management.
In case of two or more competing projects (each one
having a discounted payback period less than the maximum set by the
management), the project having the shortest discounted payback period would be
selected.
Terminal Value Method
Under this method, it is assumed that each cash flow
is re-invested in another project at a certain rate of interest. It is also
assumed that each cash inflow is re-invested elsewhere immediately until the
termination of the project. In other words, under this method, the cash inflows
are compounded forward rather than discounting them backward as followed in NPV
method. These compounded values are to be calculated till the termination of
the project and total of all the terminal values is called Terminal
Value of the Project. The compounded values are then discounted
at an appropriate discount rate (normally, cost of capital) to find out the
present value. This present value is compared with the initial cash outflow to
arrive at the Modified NPV of the project and
to find out the justifiability of the project.
Therefore, Modified NPV = PV of TV of the Project –
Initial Cash Outflow
Decision criteria:
In case of a single project, the project will be accepted
if the Modified NPV is positive. In case of two or more competing projects, the
project with the highest Modified NPV would be selected.
Equivalent NPV Concept
Equivalent NPV means Annualised
Net Benefit. Equivalent NPV method should be adopted when
economic lives of two or more projects are different.
Formulas for Equivalent NPV (ENPV)
|
1. |
ENPV = |
Average / Annual CIAT – Average / Annual Cash
Outflow (i.e. ACO) |
|
|
Where, |
|
|
|
ACO = |
Initial Investment x Capital Recovery Factor (i.e.
CRF) |
|
|
CRF = |
1 ÷ (PV of annuity of Rs 1 for the life of the
project at the given discount rate) |
|
2. |
ENPV |
(NPV of the project) ÷ (PV of annuity of Rs 1 for
the life of the project at the given discount rate) |
|
3. |
ENPV |
NPV of the project x Capital Recovery Factor |
Types of cash flows
Cash flows associated with an investment proposal may
be classified into three components:
(i)
Initial cash outflow (i.e. initial investment)
(ii)
Annual operating cash inflow (i.e. cash inflow after tax, in short CIAT),
and
(iii) Terminal cash inflow
Initial investment – Initial investment comprises:
(a) Initial cost of the new project / asset,
(b) Installation charges, and
(c) Working capital introduced.
Cash inflow after tax (CIAT)
CIAT is calculated using either of the following two
formulas:
|
1. |
CIAT = |
PAT + Depreciation + Interest (1 – t) [Note: Here PAT is after charging interest] |
|
2. |
CIAT = |
EBIT (1 – t) + Depreciation |
If CIBT (Cash inflow before tax) is given in the
problem along with depreciation, etc., CIAT will be calculated as follows:
STEP 1:
|
PBT = |
CIBT – Depreciation |
STEP 2:
|
PAT = |
PBT – Tax |
STEP 3:
|
CIAT = |
PAT + Depreciation + Interest (1 – t) |
Therefore, if CIBT is given and there is no interest
cost,
|
CIAT = |
[(CIBT – D) – T] + D; where, D = Depreciation and, T = Tax |
Terminal cash inflow
Terminal cash inflow consists of
(i)
Working capital recovered, and
(ii)
Net cash inflow from the sale of scrap.
Net cash inflow from the sale of scrap can be
calculated as follows:
A. If the Income-Tax Rules regarding depreciation on block of assets are not required to be
followed –
|
Particulars |
Rs |
|
Proceeds from the sale of scrap |
××× |
|
ADD: Tax on capital loss [(Cost of acquisition – Sale proceeds) x Rate of capital gains tax] |
××× |
|
LESS: Tax on capital gain [(Sale proceeds – Cost of acquisition) x Rate of capital gains tax] |
××× |
|
LESS: Tax on profit on sale of asset [(Cost of acquisition – Book value of the asset) × Normal rate of tax |
××× |
|
NET CASH INFLOW FROM THE SALE OF SCRAP |
××× |
Important note:
Under straight line method of depreciation, book value
and sale proceeds in the terminal year of the project are same. Therefore,
there will be no tax benefit or tax loss on capital loss or capital gain
respectively under the straight line method of depreciation.
B. If the Income-Tax Rules regarding depreciation on block of assets are required to be
followed –
|
Particulars |
Rs |
|
Proceeds from the sale of scrap |
××× |
|
ADD: Tax on short term capital loss [STCL x Normal rate of tax] |
××× |
|
LESS: Tax on short term capital gain [STCG x Normal rate of tax] |
××× |
|
NET CASH INFLOW FROM THE SALE OF SCRAP |
××× |
Important notes:
1. Under section 50 of the Income Tax Act, there cannot
be any long term capital gain / loss on disposal of depreciable assets.
2. There will be short term capital gain / loss on
disposal of depreciable assets only in case of the following two situations –
Situation one:
Under section 50(1), there will be short term capital
gain, if on the last day of the previous year WDV of the block of assets is
zero. No depreciation will be allowed under this situation.
Situation two:
Under section 50(2), there will be short term capital
gain or loss, if the block of assets is empty on the last day of the previous
year. No depreciation will be allowed under this situation.
3. There will be no short term capital gain / loss if the
disposal of depreciable assets does not fall under any of the above two
situations. In this case depreciation will be allowed under section 32 of the
Income Tax Act.
Capital rationing
Capital rationing means distribution of limited
capital in favour of more acceptable proposals. It refers to a situation where
a firm is not in a position to invest in all the available profitable projects
due to the limited financial resources in the form of capital. Under this
situation a firm is compelled to reject some of the viable projects having
positive net present value because of shortage of funds. Therefore, the firm
has to select a feasible combination of proposals that will give the maximum
return to the shareholders by maximising the total net present value from the
available projects.
There are two methods of capital rationing under the
two different situations in terms of divisibility of the projects. The methods
of capital rationing are:
1. Capital rationing when projects are divisible, and
2. Capital rationing when projects are indivisible.
Capital rationing when projects are divisible
Selection of projects under this situation will
require the taking of the following steps:
STEP − 1:
Calculate the profitability index (PI) or the internal
rate of return (IRR) of each project.
STEP − 2:
Rank the projects in descending order of PI or IRR
calculated in step − 1 above.
STEP − 3:
Prepare a statement showing the cumulative initial
investment against the projects arranged in order of their rankings.
STEP − 4:
Select the optimal combination of the projects in such
a way that the total amount of initial investment required for all the selected
projects is equal to the total available investible capital. Since the projects
are divisible, the last project in terms of the rankings of the projects may be
selected partially utilising the balance of the available capital.
Capital
rationing when projects are indivisible
Selection of projects under this situation will
require the taking of the following steps:
STEP − 1:
Make a list of feasible combinations of the projects
in such a way that the total amount of initial investment required for any of
the combinations does not exceed the total fund available for investment and at
the same time maximum possible amount of the available investible fund is
utilised for each of the combinations of the projects.
STEP − 2:
Select the combination of the projects whose aggregate NPV is the maximum and consider it as the optimal project mix.
Part B
Illustration: 1
From the following data find out the IRR of a project:
Initial investment = Rs 1, 00,000
Cash flows for:
|
1st
year |
Rs
30,000 |
|
2nd
year |
Rs
30,000 |
|
3rd
year |
Rs
40,000 |
|
4th
year |
Rs
45,000 |
Illustration: 2
PQR Ltd. is evaluating a project that has the following cash flow stream
associated with it.
|
Year |
Cash
Flow (Rs in lakhs) |
|
0 |
(-)
120 |
|
1 |
(-)
80 |
|
2 |
20 |
|
3 |
60 |
|
4 |
80 |
|
5 |
100 |
|
6 |
120 |
The cost of capital for the company is 15%.
Find the Present Value of Cost (PVC). Find out also the Terminal Value
(TV) of the cash inflows. Show the MIRR.
Illustration: 3
Following information is available from XYZ Ltd.
regarding a project:
Initial outlay Rs 2, 00,000
Project life 5 years
Net cash inflow Rs 80,000 each of 5 years
Cost of capital @ 10%
Expected rate of interest are:
|
End
of the year |
Percentage |
|
1 |
6% |
|
2 |
6% |
|
3 |
8% |
|
4 |
8% |
Evaluate the proposal using Terminal Value method.
Illustration: 4
The directors of Beta Limited are contemplating the
purchase of a new machine to replace a machine which has been in operation in the factory for the
last 5 years.
Ignoring interest but considering tax at 50% of net earnings, suggest
which of the two alternatives should be preferred. The following are the
details:
|
Particulars |
Old
Machine |
New
Machine |
|
Purchase
price |
Rs
40,000 |
Rs
60,000 |
|
Estimated
life of machine |
10
years |
10
years |
|
Machine
running hours p.a. |
2,000 |
2,000 |
|
Units
per hour |
24 |
36 |
|
Wages
per running hour |
Rs
3 |
Rs
5.25 |
|
Power
p.a. |
Rs
2,000 |
Rs
4,500 |
|
Consumables
stores p.a. |
Rs
6,000 |
Rs
7,500 |
|
Other
charges p.a. |
8,000 |
9,000 |
|
Materials
cost per unit |
Rs
0.50 |
Rs
0.50 |
|
Selling
price per unit |
Rs
1.25 |
Rs
1.25 |
You may assume that the above information regarding sales and cost of
sales will hold good, throughout the economic life of each of the machines.
Depreciation has to be charged according to straight-line method.
Illustration: 5
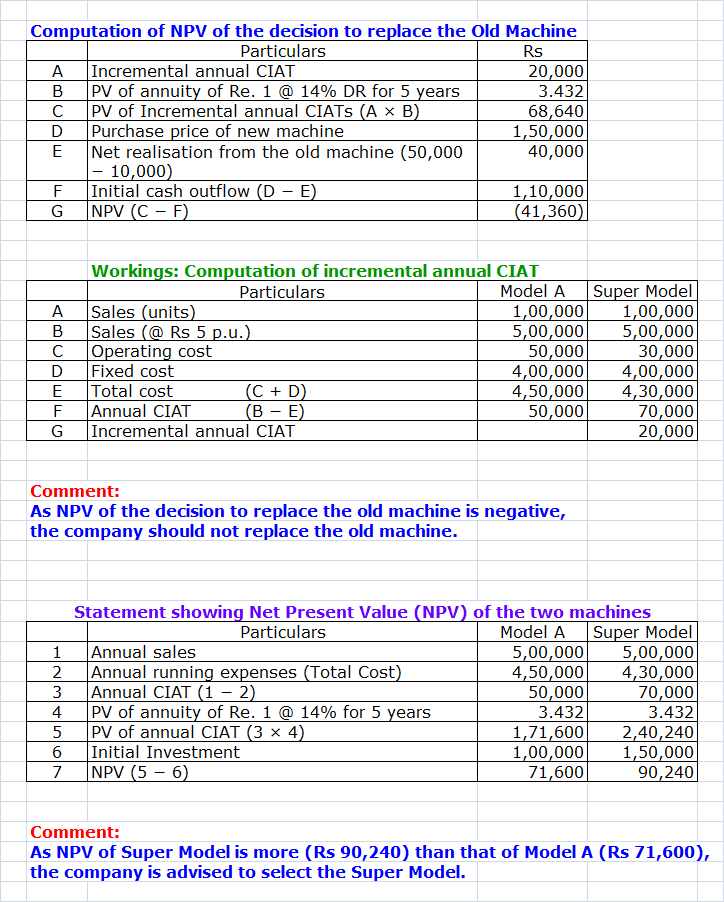
A company has just installed a machine Model A for the manufacture of a new product at capital cost of Rs 1, 00,000. The annual operating costs are estimated at Rs 50,000 (excluding depreciation) and these costs are estimated on the basis of an annual volume of 1, 00,000 units of production. The fixed costs at this volume of 1, 00,000 units of output will amount to Rs 4, 00,000 per annum. The selling price is Rs 5 per unit of output. The machine has a five year life with no residual value.
The company has now come across another machine called Super Model which is capable of giving, the same volume of production at an estimated annual operating costs of Rs 30,000 exclusive of depreciation. The fixed costs will however, remain the same in value. This machine also will have a five year life with no residual value. The capital cost of this machine is Rs 1, 50,000.
The company has an offer for the sale of the machine Model A (which has just been installed) at Rs 50,000 and the cost of removal thereof will amount to Rs 10,000. Ignore tax.
In view of the lower operating cost, the company is desirous of dismantling of the machine Model A and installing the Super Model Machine. Assume that Model A has not yet started commercial production and that the time lag in the removal thereof and the installation of the Super Model machine is not material.
The cost of capital is 14% and the P.V. Factors for each of the five years respectively are 0.877, 0.769, 0.675, 0.592 and 0.519.
State whether the company should replace machine Model A by installing the Super Model machine.
Will there be any change in your decision if the Model
A machine has not been installed and the company is in the process of
consideration of selection of either of the two models of the machine? Present
suitable statement to illustrate your answer.
Illustration: 6
Techtronics Ltd., an existing
company, is considering a new project for manufacture of pocket video games
involving a capital expenditure of Rs 600 lakhs and working capital of Rs 150
lakhs. The capacity of the plant is for an annual production
of 12 lakh units and capacity utilisation during the 6-year working life of the
project is expected to be as indicated below.
|
Year |
Capacity Utilisation (%) |
|
1 |
33 1/3 % |
|
2 |
66 2/3 % |
|
3 |
90% |
|
4 - 6 |
100% |
The average price per unit of the product is expected to be Rs 200 netting a contribution of 40%. Annual fixed costs, excluding depreciation, are estimated to be Rs 480 lakhs per annum from the third year onwards; for the first and second year it would be Rs 240 lakhs and Rs 360 lakhs respectively. The average rate of depreciation for tax purposes is 33 1/3 % on the capital assets. No other tax reliefs are anticipated. The rate of income-tax may be taken at 50%.
At the end of the third year, an additional investment of Rs 100 lakhs would be required for working capital.
The company, without taking into account the effects of financial leverage, has targeted for a rate of return of 15%.
You are required to indicate whether the proposal is viable giving your working notes and analysis.
Terminal value for the fixed assets
may be taken at 10% and for the current assets at 100%. Calculation may be
rounded off to lakhs of rupees. For the purpose of your calculations, the
recent amendments to tax laws with regard to balancing charge may be ignored.
Illustration: 7
Dey’s Chemical, a chemical company, is
considering replacing an existing machine with one costing Rs 65,000.
The existing machine was originally purchased two years ago for Rs 28,000 and
is being depreciated by the straight line method over its seven-year life period.
It can currently be sold for Rs 30,000 with no removal costs. The new machine
would cost Rs 10,000 to install and would be depreciate over five years. The
management believes that the new machine would have a salvage value of Rs 5,000
at the end of year 5. The management also estimates an increase in net working
capital requirement of Rs 10,000 as a result of expanded operations with the
new machine. The firm is taxed at a rate of 55% on normal income and 30% on
capital gains. The company’s expected after-tax profits for next 5 years with
existing machine and with new machine are given as follows:
|
|
Expected after-tax profit (Rs) |
|
|
Year |
With existing machine |
With new machine |
|
1 |
2,00,000 |
2,16,000 |
|
2 |
1,50,000 |
1,50,000 |
|
3 |
1,80,000 |
2,00,000 |
|
4 |
2,10,000 |
2,40,000 |
|
5 |
2,20,000 |
2,30,000 |
(a) Calculate the net
investment required by the new machine.
(b) If the company’s
cost of capital is 15%, determine whether the new machine should be purchased.
Illustration: 8
A Company is considering two mutually exclusive projects. Project K will require an initial cash investment in machinery of Rs 2, 68,000. It is anticipated that the machinery will have a useful life of ten years at the end of which its salvage will realise Rs 20,500. The project will also require an additional investment in cash, Sundry debtors and stock of Rs 40,000. At the end of five years from the commencement of the project balancing equipment for Rs 45,000 has to be installed to make the unit workable. The cost of additional machinery will be written off to depreciation over the balance life of the project. The project is expected to yield a net cash flow (before depreciation) of Rs 1, 00,000 annually.
Project R, which is the alternative one under consideration, requires an investment of Rs 3, 00,000 in machinery and (as in Project K) investment in current assets of Rs 40,000. The residual salvage value of the machinery at the end of its useful life of ten years is expected to be Rs 25,000. The annual cash inflow (before depreciation) from the project is worked at Rs 80,000 p.a. for the first five years and Rs 1, 80,000 per annum for the next five years.
Depreciation is written off by the Company on sum-of-the years’ digits method. Income tax rate is 50%. A minimum rate of return has been calculated at 16%. The present value of Re 1 at interest rate of 16% p.a. is 0.86, 0.74, 0.64, 0.55, 0.48, 0.41, 0.35, 0.30, 0.26 and 0.23 for years 1 to 10 respectively.
Which Project is better? Assuming no capital
gains taxes, calculate the Net Present Value of each Project.
Illustration: 9
A product is currently manufactured
on a machine that is not fully depreciated for tax purposes and has
a book value of Rs 70,000. It was purchased for Rs 2, 10,000 twenty years ago.
The costs of the product are as follows:
|
|
Unit Cost (Rs) |
|
Direct labour |
28 |
|
Indirect labour |
14 |
|
Other variable overheads |
10.5 |
|
Fixed overheads |
17.5 |
|
Total |
70 |
In the past year 10,000 units were produced. It is expected that with suitable repairs the old machine can be used indefinitely in future. The repairs are expected to average Rs 75,000 per year.
An equipment manufacturer has offered
to accept the old machine as a trade in for a new machine. The new machine
would cost Rs 4, 20,000 before allowing for Rs 1, 05,000 for the old equipment.
The Project costs associated with the new machine are as follows:
|
|
Unit Cost (Rs) |
|
Direct labour |
14 |
|
Indirect labour |
21 |
|
Other variable overheads |
7 |
|
Fixed overheads |
22.75 |
|
Total |
64.75 |
The fixed overhead costs are
allocations for other departments plus the depreciation of the machine. The old
machine can be sold now for Rs 50,000 in the open market. The new
machine has an expected life of 10 years and salvage value of Rs 20,000 at that
time. The current corporate income tax rate is assumed to be 50%. For tax
purposes cost of the new machine and the book value of the old machine may be
depreciated in 10 years. The minimum required rate is 10%. It is expected that
the future demand of the product will stay at 10,000 units per year. The
present value of an annuity of Re 1 for 9 years @ 10% discount rate is 5.759.
The present value of Re 1 received at the end of 10th year @10% discount
rate is 0.386. Should the new machine be purchased?
Illustration: 10
Ram Ltd. specialise in the manufacture of novel transistors. They have recently developed technology to design a new radio transistor capable of being used as an emergency lamp also. They are quite confident of selling all the 8,000 units that they would be making in a year. The capital equipment that would be required will cost Rs 25 lakhs. It will have an economic life of 4 years and no significant terminal salvage value.
During each of the first four years
promotional expenses are planned as under:
|
Year |
1 |
2 |
3 |
4 |
|
Advertisement (Rs) |
1,00,000 |
75,000 |
60,000 |
30,000 |
|
Others (Rs) |
50,000 |
75,000 |
90,000 |
1,20,000 |
|
Variable cost of production and selling expenses: Rs
250 per unit |
||||
Additional fixed operating costs incurred because of this new product are budgeted at Rs 75,000 per year.
The company’s profit goals call for a discounted rate of return of 15% after taxes on investments on new products. The income tax rate on an average works out to 40%. You can assume that the straight line method of depreciation will be used for tax and reporting.
Work out an initial selling price per unit of the product that may be fixed for obtaining the desired rate of return on investment.
Present value of annuity of Re 1
received or paid in a steady stream throughout 4 years in the future at 15% is
2.8550.
Illustration: 11
Following are the data on a capital project (Project M) being
evaluated by the management of PKJ Ltd.:
|
|
Project M |
|
Annual cost saving |
Rs 40,000 |
|
Useful life |
4 years |
|
IRR |
15% |
|
Profitability Index (PI) |
1.064 |
|
NPV |
? |
|
Cost of capital |
? |
|
Cost of project |
? |
|
Pay back |
? |
|
Salvage value |
0 |
Find the missing values considering the following table of
discount factor only:
|
Discount Rate |
15% |
14% |
13% |
12% |
|
1 year |
0.869 |
0.877 |
0.885 |
0.893 |
|
2 years |
0.756 |
0.769 |
0.783 |
0.797 |
|
3 years |
0.658 |
0.675 |
0.693 |
0.712 |
|
4 years |
0.572 |
0.592 |
0.613 |
0.636 |
|
|
2.855 |
2.913 |
2.974 |
3.038 |
Illustration: 12
Packagers Limited is considering two mutually exclusive
projects. Both require an initial cash outlay of Rs 10,000 each for machinery and have a life of 5 Years. The
Company’s required rate of return is 10% and it pays tax at 50%. The projects
will be depreciated on a straight-line basis. The net cash flows (before taxes)
expected to be generated by the projects and the present value (PV) factor (at
10%) are as follows:
|
|
Year 1 |
Year 2 |
Year 3 |
Year 4 |
Year 5 |
|
Project: 1 (Rs) |
4,000 |
4,000 |
4,000 |
4,000 |
4,000 |
|
Project: 2 (Rs) |
6,000 |
3,000 |
2,000 |
5,000 |
5,000 |
|
PV Factor (at 10%) |
0.909 |
0.826 |
0.751 |
0.683 |
0.621 |
You are
required to calculate:
I. The Pay Back Period
of each project;
II. The NPV of each
project; and
III. The Profitability Index (PI) of each
project.
Illustration: 13
Alliance Limited is considering a
proposal of investing in a project requiring a capital outlay of Rs 2, 00,000. Forecast for annual income after depreciation but before tax
is as follows:
|
Year |
Rs |
|
1 |
1,00,000 |
|
2 |
1,00,000 |
|
3 |
80,000 |
|
4 |
80,000 |
|
5 |
40,000 |
Depreciation may be taken as 20% on original cost and
taxation at 50% of net income. You are required to evaluate the project according to each of the following
methods:
a) Pay-back
method;
b) Rate
of return on original investment method;
c) Rate
of return on average investment method;
d) Discounted
cash flow method taking cost of capital as 10%;
e) Net
present value index method;
f)
Internal rate of
return method; and
g) Modified
internal rate of return method.
















I have read this note .this note is very useful for all CA,CMA Student .
ReplyDeleteI read this article thoroughly and i understood each and everything. It is very helpful for my upcoming exam.
ReplyDelete